이분 탐색
이분 탐색은 탐색 기법의 하나입니다. 탐색 범위를 두 부분으로 분할 하며 탐색한다 하여 이분 탐색이라고 이름 지어졌습니다. 이분 탐색의 핵심은 왼쪽 경계, 오른쪽 경계, 가운데를 어떻게 두느냐가 핵심입니다. 설명의 편의를 위해 left(=왼쪽 경계) , right(=오른쪽 경계) , mid(=가운데) 라고 하겠습니다.
탐색 방법은 아래와 같습니다.
1. left 값을 탐색 범위의 최소 인덱스로 지정합니다.
2. right 값을 탐색 범위의 최대 인덱스로 지정합니다.
3. mid의 값을 (left + right)/2로 지정합니다.
4. 찾으려는 값이 mid와 같은지 비교해줍니다. (같을 시 반복 종료)
5. 찾으려는 값이 mid보다 높다면 left = mid + 1로 초기화한 후 1 ~ 4의 step을 반복합니다.
6. 찾으려는 값이 mid보다 낮다면 right = mid - 1로 초기화한 후 1 ~ 4의 step을 반복합니다.
이러한 방법으로 탐색을 진행하면 O( log(n))의 시간 복잡도가 걸립니다.
아래는 이분 탐색의 시각화입니다.
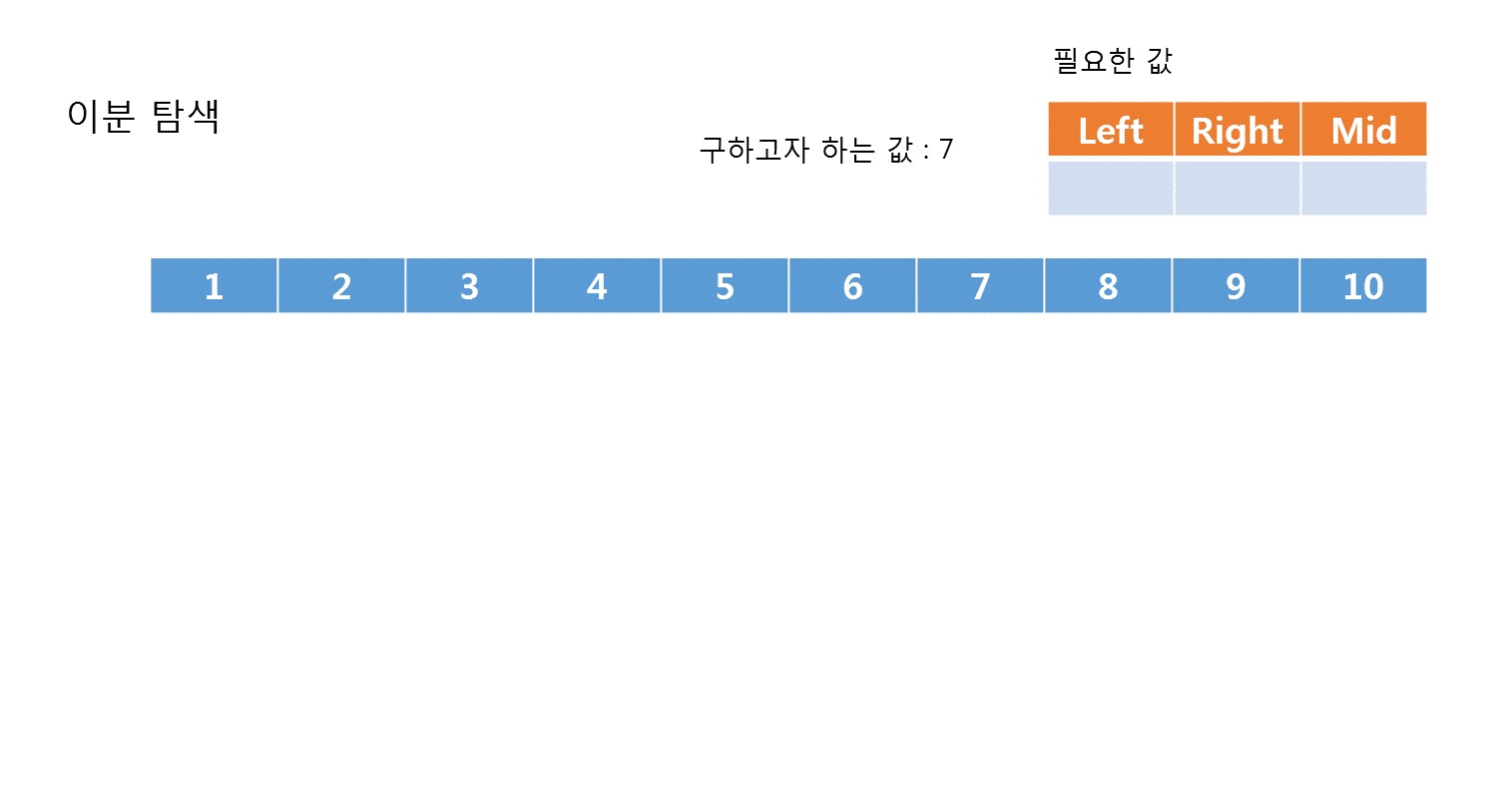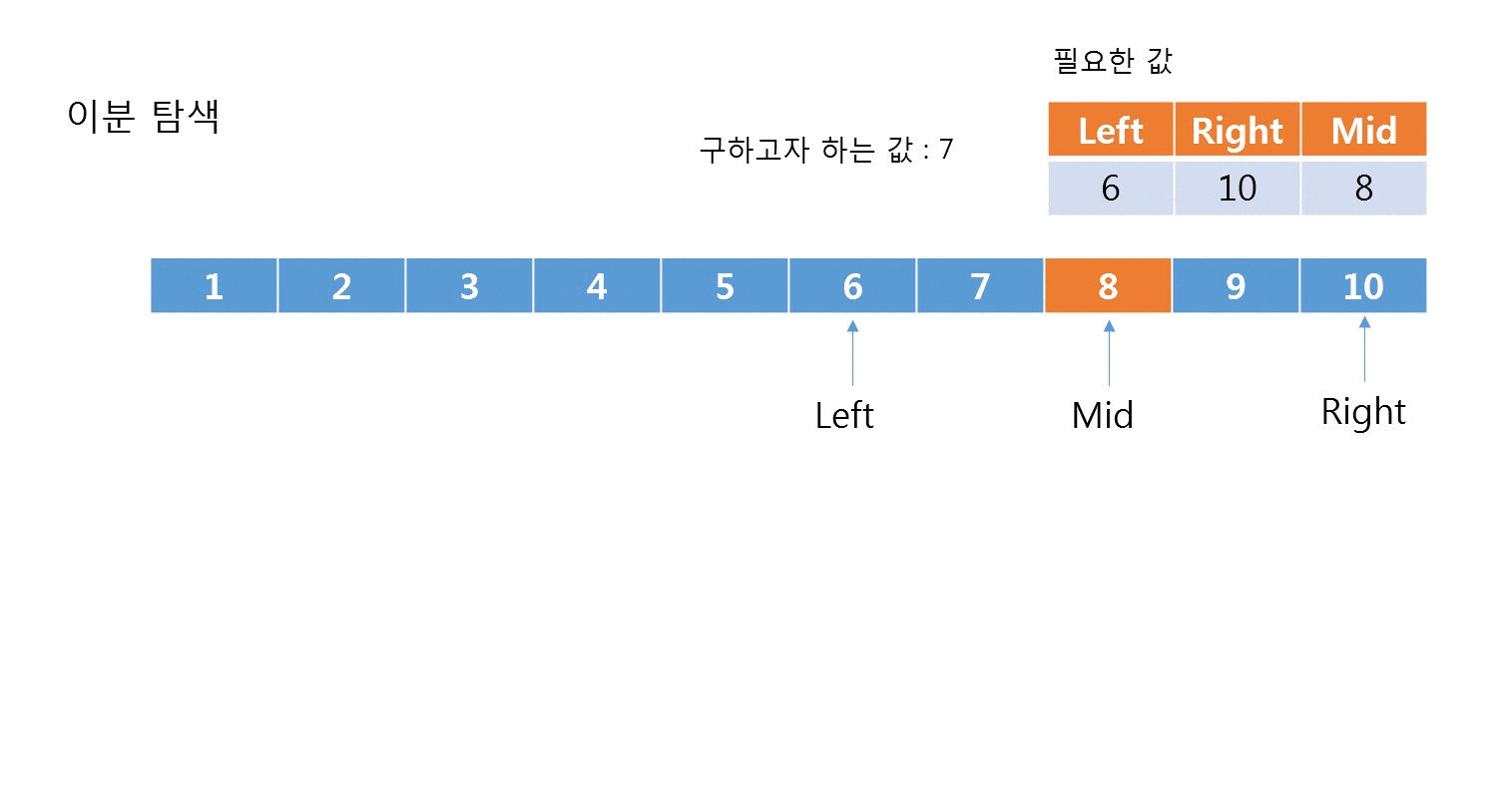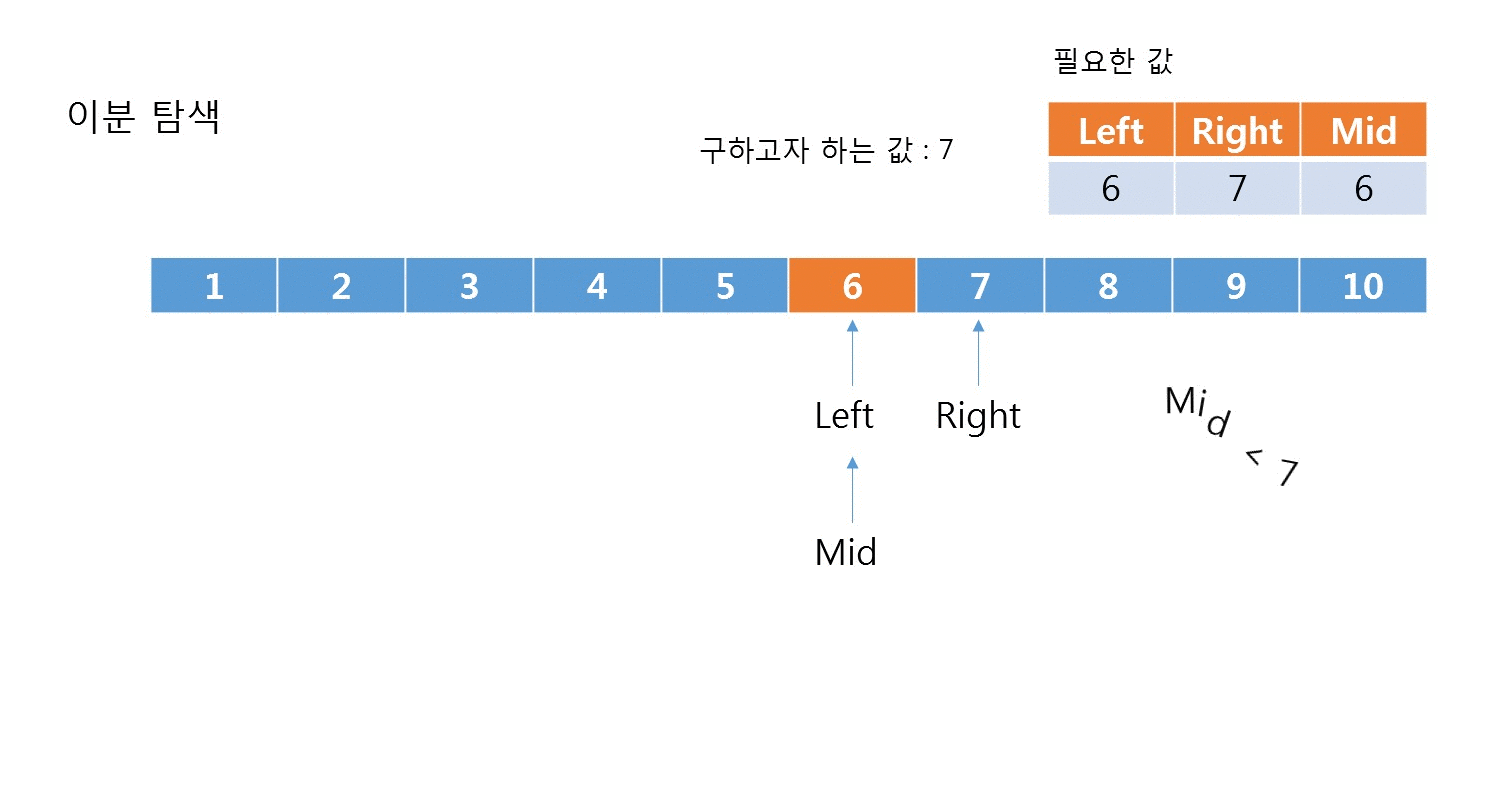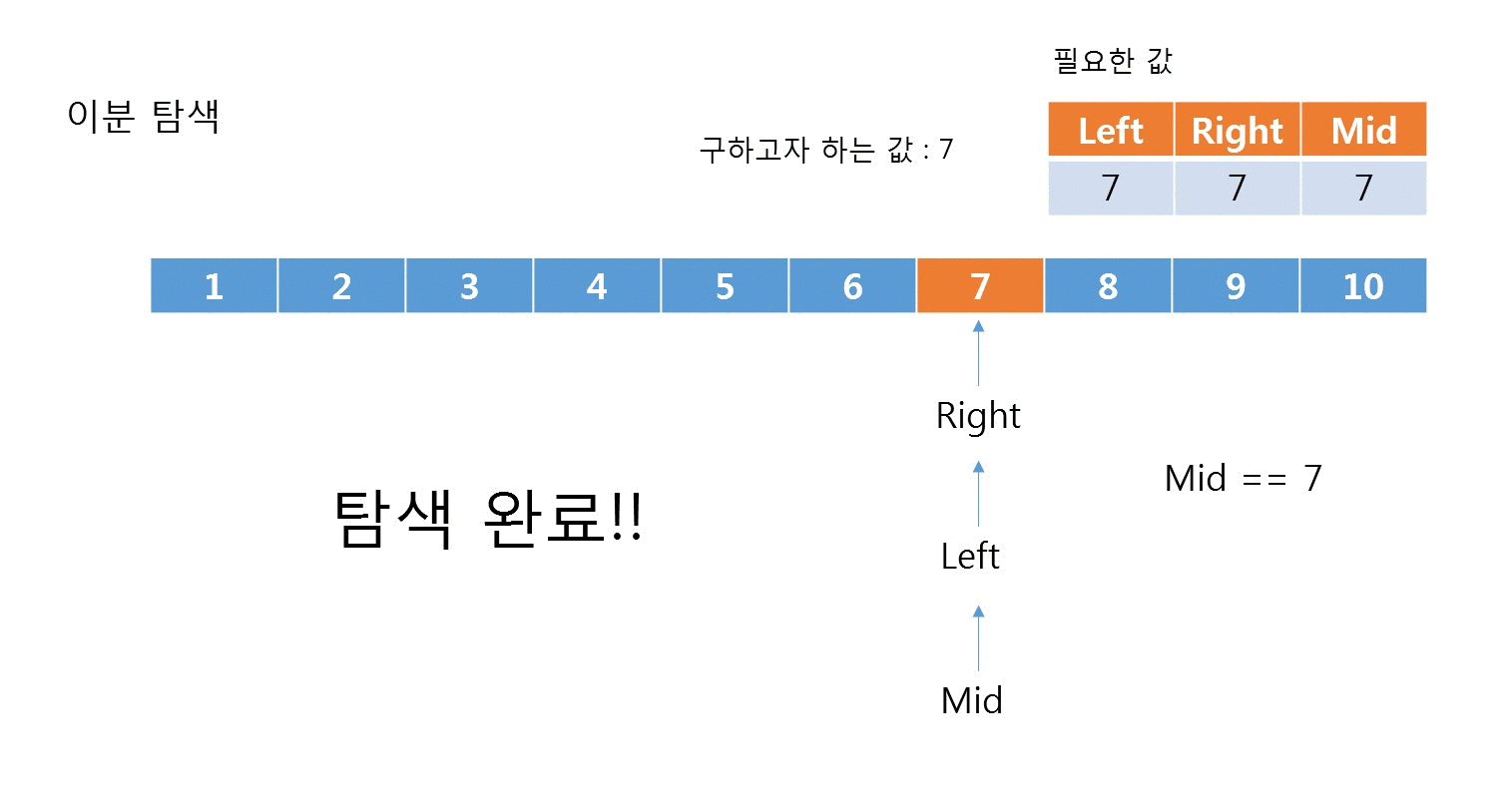
[코드]
#include <iostream>
using namespace std;
int main(void){
int target; // 찾으려는 값
int result = 0; //target 인덱스 값
int index_arr[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
scanf("%d", &target);
int left = index_arr[0];
int right = index_arr[9];
while (left <= right){
int mid = (left + right) / 2;
if (index_arr[mid] > target){
right = mid - 1;
}
else if (index_arr[mid] < target){
left = mid + 1;
}
else if (index_arr[mid] == target)
{
result = mid;
break;
}
}
printf("%d\n", result);
return 0;
}
'algorithm > 이론' 카테고리의 다른 글
| 서로소 집합(Disjoint Set, Union-Find) (0) | 2021.04.15 |
|---|---|
| 최소 신장 트리(Minimum Spanning Tree) (0) | 2021.04.14 |
| (C++ STL) priority_queue (0) | 2020.10.18 |
| (C++ STL) lower_bound, upper_bound (0) | 2020.10.10 |

